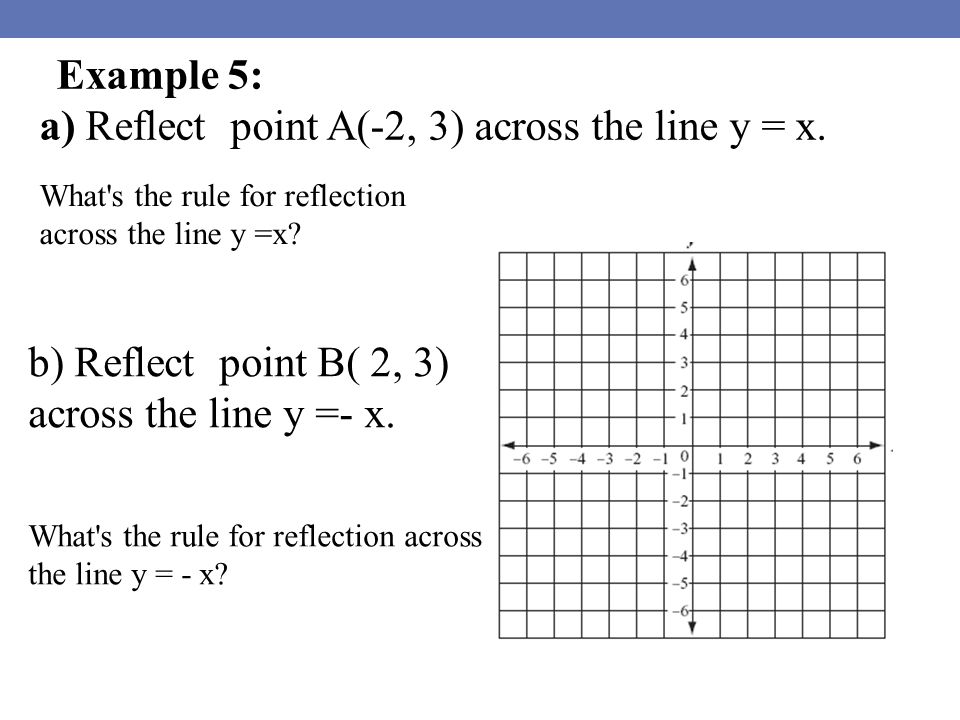
A reflection across the line y = x switches the x and ycoordinates of all the points in a figure such that (x, y) becomes (y, x) Triangle ABC is reflected across the line y = x to form triangle DEF Triangle ABC has vertices A (2, 2), B (6, 5) and C (3, 6) Triangle DEF has vertices D (2, 2), E (5, 6), and F (6, 3)SWBAT reflect an image over y=xA reflection in a line produces a mirror image in which corresponding points on the original shape are always the same distance from the mirror line The reflected image has the same size as the original figure, but with a reverse orientation Examples of transformation geometry in the coordinate plane Reflection over y axis (x, y) ( x, y)
How To Reflect A Graph Through The X Axis Studypug
Reflection across y=x example
Reflection across y=x example- 23 Coordinate Geometry Ihe following steps explain how to reflect point A across the line y = x Step 1 Draw line € through A(5,1) perpendicular to the line y = x The slope ofy = xis 1, so the slope of line € is 1 • (—1), or —1 Step 2 From A, move two units left and two units up to y = xReflection Transformations in 2Space Let such that and suppose that we want to reflect across the axis as illustrated Thus the coordinate of our vector will be the opposite to that of our image The following equations summarize our image Thus our standard matrix is , and in form we get that Of course there are other types of reflection



Reflection An Isometry Or Rigid Motion In Which A Figure Is Flipped Giving Its Image An Opposite Orientation Ppt Download
The following diagram shows how to reflect points and figures on the coordinate plane Examples shown are reflect across the xaxis, reflect across the yaxis, reflect across the line y = x Scroll down the page for more examples and solutions on reflection in the coordinate plane Geometry Reflection Show Stepbystep SolutionsReflection about the line y=x Once students understand the rules which they have to apply for reflection transformation, they can easily make reflection transformation of a figure For example, if we are going to make reflection transformation of the point (2,3) about xaxis, after transformation, the point would be (2,3)Example 3 Triangle PQR has the vertices P(2, 5), Q(6, 2) and R(2, 2) Find the vertices of triangle P'Q'R' after a reflection across the xaxis Then graph the triangle and its image Solution Step 1 Apply the rule to find the vertices of the image
We need an m x n matrix A to allow a linear transformation from Rn to Rm through Ax = b In the example, T R2 > R2 Hence, a 2 x 2 matrix is needed If we just used a 1 x 2 matrix A = 1 2, the transformation Ax would give us vectors in R1Enjoy the videos and music you love, upload original content, and share it all with friends, family, and the world onFor a reflection over the x − axis y − axis line y = x Multiply the vertex on the left by 1 0 0 − 1 − 1 0 0 1 0 1 1 0
The assumption can br made that a point (x,y) has a reflection (y,x) Now look at the point (4,0) and its reflection (0,4) The definition of reflection explains that the reflection of a point P, P', over a line, y=x, will result in a segment connecting P and P' at aReflections in Math Applet Interactive Reflections in Math Explorer Demonstration of how to reflect a point, line or triangle over the xaxis, yaxis, or any line x axis y axis y = x y = x Equation Point Segment Triangle Rectangle y =Reflections and Rotations We can also reflect the graph of a function over the xaxis (y = 0), the yaxis(x = 0), or the line y = x Making the output negative reflects the graph over the xaxis, or the line y = 0 Here are the graphs of y = f (x) and y = f (x)




Lesson 10 5 Transformations 1 Lesson 10 5 Transformations Ppt Download



Schoolwires Henry K12 Ga Us Cms Lib08 Ga Centricity Domain 26 7th and 8th grade math 8th grade flexbook Unit 1 sections 1 23 1 4 rules for reflections Pdf
Solution Step 1 Extend a perpendicular line segment from to the reflection line and measure it Since the reflection line is perfectly horizontal, a line perpendicular to it would be perfectly vertical Created with Raphaël Step 2 Extend the line segmentAfter it reflection is done concerning xaxis The last step is the rotation of y=x back to its original position that is counterclockwise at 45° Example A triangle ABC is given The coordinates of A, B, C are given as A (3 4) B (6 4) C (4 8) Find reflected position of triangle ie, to the xaxis Solution The a point coordinates afterRelated Pages Properties Of Reflection Transformation More Lessons On Geometry What is Reflection?




Reflection Rules How To W 25 Step By Step Examples




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines
A reflection can occur across any line, it is not limited to the three lines discussed previously The example below demonstrates a reflection that is not specific to the axes or the line y = x Examine the drawing below to see the relationship between theIn a reflection transformation, all the points of an object are reflected or flipped on a line called the axis of reflection or line of reflection Example A reflection is defined by the axis of symmetry or mirror lineIn the above diagram, the mirror line is x = 3This lesson is presented by Glyn CaddellFor more lessons, quizzes and practice tests visit http//caddellpreponlinecomFollow Glyn on twitter http//twitter




Reflection Over The Line Y X Youtube




How To Graph Reflections Across Axes The Origin And Line Y X Video Lesson Transcript Study Com
Reflection over the line y = − x A reflection in the line y = x can be seen in the picture below in which A is reflected to its image A' The general rule for a reflection in the y = − xGeometry 3 people liked this ShowMe Flag ShowMe Viewed after searching for reflect over x= 1 reflection over the line y=x Reflection over y=x reflection over yaxis reflectionThis is a KS3 lesson on reflecting a shape in the line y = −x using Cartesian coordinates It is for students from Year 7 who are preparing for GCSE This page includes a lesson covering 'how to reflect a shape in the line y = −x using Cartesian coordinates' as well as a 15question worksheet, which is printable, editable and sendable




Reflections Lesson Ppt Video Online Download




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines
1) a line reflection over y =x 2) a rotation of 180° centered at (1,0) 3) a line reflection over the xaxis followed by a translation of 6 units right 4) a line reflection over the xaxis followed by a line reflection over y =1 4 In the diagram below, A′B′C′ is a transformation of ABC, and A″B″C″ is a transformation of A′B′C′Reflections across y=x Click and drag the blue dot and watch it's reflection across the line y=x (the green dot) Pay attention to the coordinates Reflection in a Line A reflection over a line k (notation r k) is a transformation in which each point of the original figure (preimage) has an image that is the same distance from the line of reflection as the original point but is on the opposite side of the line Remember that a reflection is a flip Under a reflection, the figure does not change size




Reflecting Functions Examples Video Khan Academy




Reflections In Math Formula Examples Practice And Interactive Applet On Common Types Of Reflections Like X Axis Y Axis And Lines



0 件のコメント:
コメントを投稿