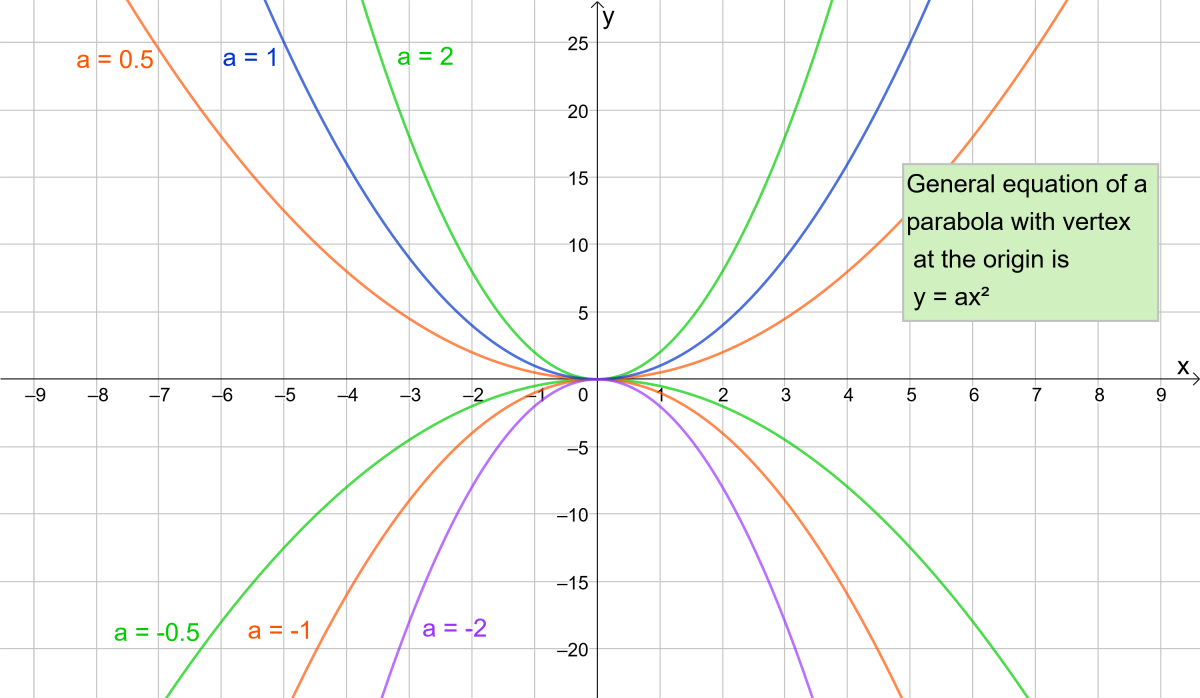
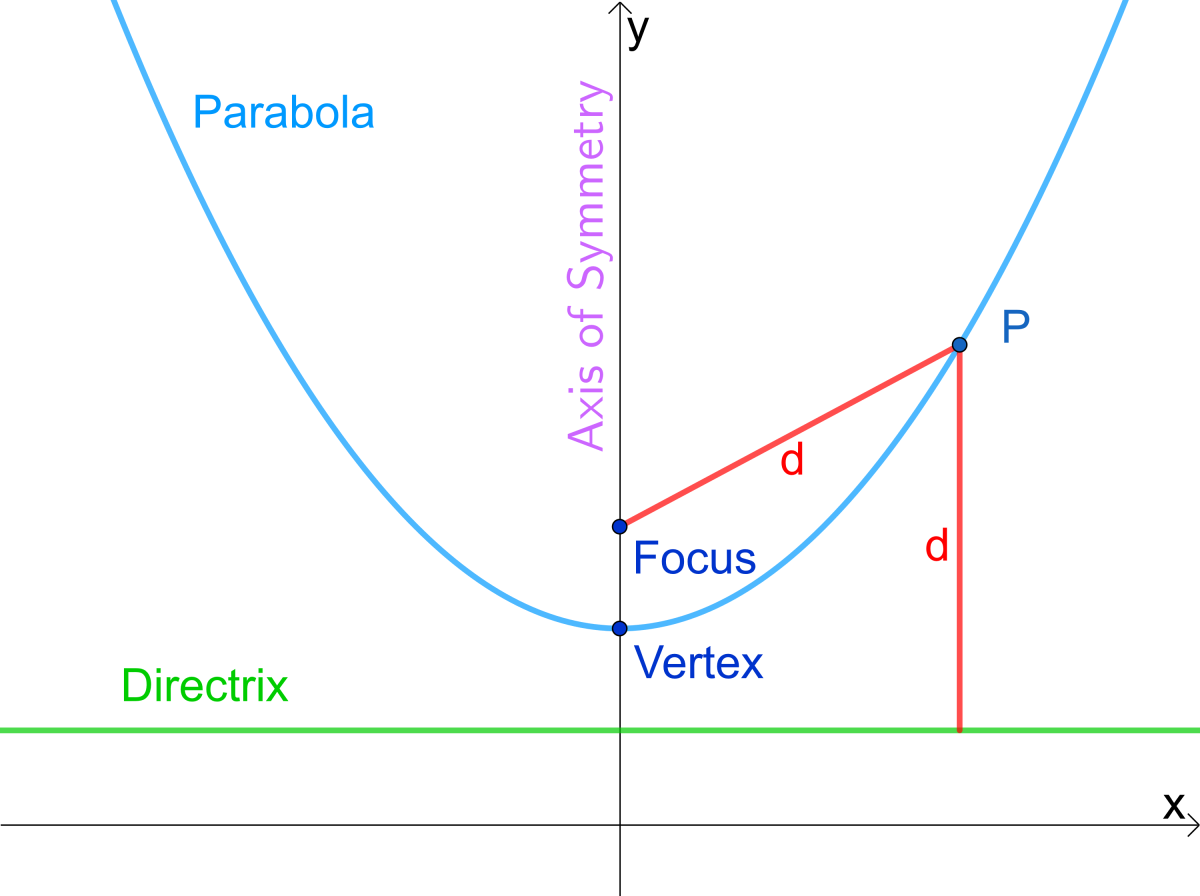
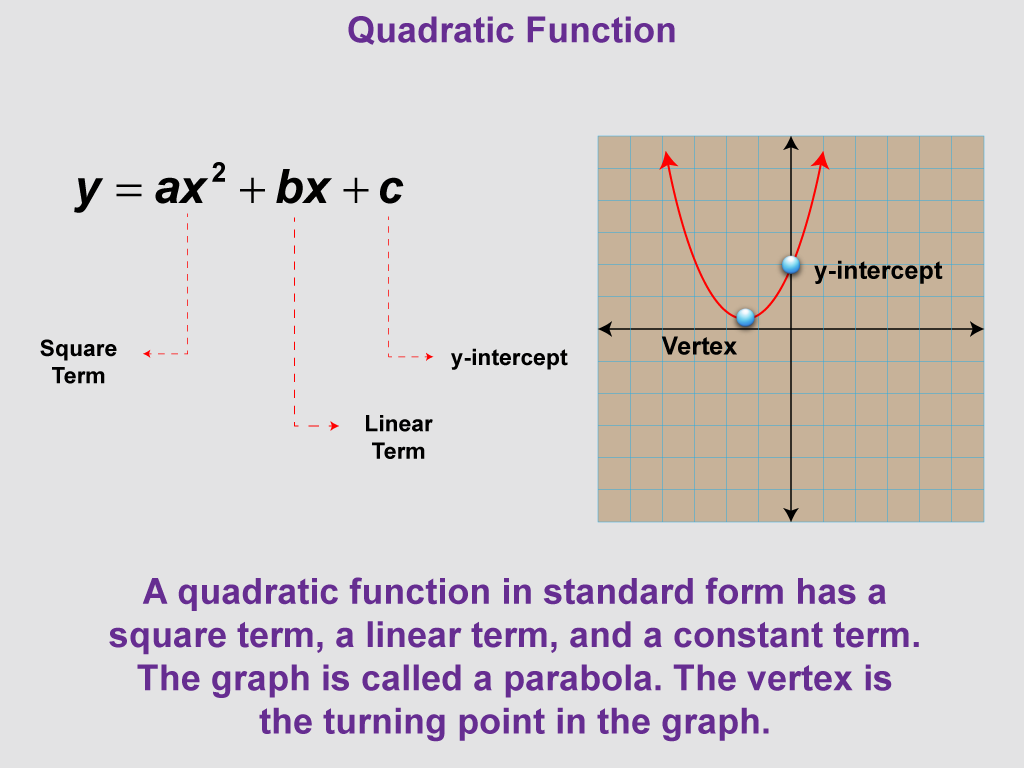
A parabola is a plane curve, every point of which has the property that the distance to a fixed point (called the focus of the parabola) is equal to the distance to a straight line (the directrix of the parabola) The distance between the focus to the directrix is called the focal parameter and denoted by \(p\)The point half inbetween the directrix and focus is known as the vertex of the parabola Below is the figure of the parabola which is shown opening up and down It also appears in the right and left the plane The parabola is written in two forms standard form and vertex form y = ax^2 bx c (standard form) a, b, and c are coefficientsThis form is called the standard form of a quadratic function The graph of the quadratic function is a Ushaped curve is called a parabola The graph of the equation y = x 2, shown below, is a parabola (Note that this is a quadratic function in standard form with a = 1 and b = c = 0) In the graph, the highest or lowest point of a parabola is

This Professor S Amazing Trick Makes Quadratic Equations Easier The New York Times
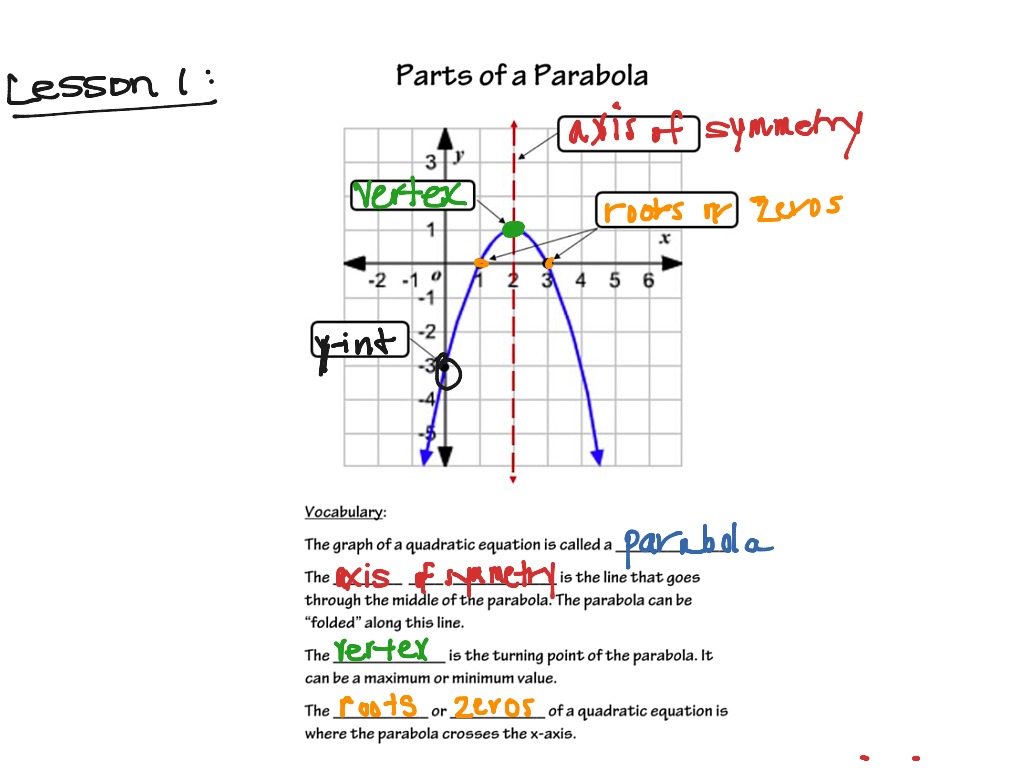
The turning point of a parabola is called
The turning point of a parabola is called-Are sometimes called xintercepts Y intercept = the y value where the parabola intersect the yaxis Vertex = the coordinates (x,y) where the parabola is "turning", this point is also called the extrema (in other words it is the spot where the parabola reaches a maximum or a minimumThe turning point form of the formula is also the velocity equation The vertex is the peak of the parabola where the velocity, or rate of change, is zero How to find the turning point of a parabola The turning point, or the vertex can be found easily by differentiation The turning point is when the rate of change is zero


5 1 The Parabola Mathematics Libretexts
Chapter 5 Functions Learners must be able to determine the equation of a function from a given graph Discuss and explain the characteristics of functions domain, range, intercepts with the axes, maximum and minimum values, symmetry, etcThe point where the parabola intersects its axis of symmetry is called the "vertex" and is the point where the parabola is most sharply curved The distance between the vertex and the focus, measured along the axis of symmetry, is the "focal length"9 Challenge #1 Drag the blue points to create a parabola that meets these requirements (1) Vertex below the $$ x axis (2) Concave up (3) One positive $$ x intercept (4) One negative $$ x intercept (5) Line of symmetry at $$ x = 2 10 Challenge #2
A General Note Interpreting Turning Points A turning point is a point of the graph where the graph changes from increasing to decreasing (rising to falling) or decreasing to increasing (falling to rising) A polynomial of degree n will have at most n – 1 turning pointsMy teacher told me that form the equation of parabola y D 4 a = a ( x b 2 a) 2 So , to find vertex of turning point , Make y = 0 and x = 0Vertex The turning point, or the point where the parabola reverses its direction 2 Axis of Symmetry The line parallel to the axis of the parabola that passes through the vertex
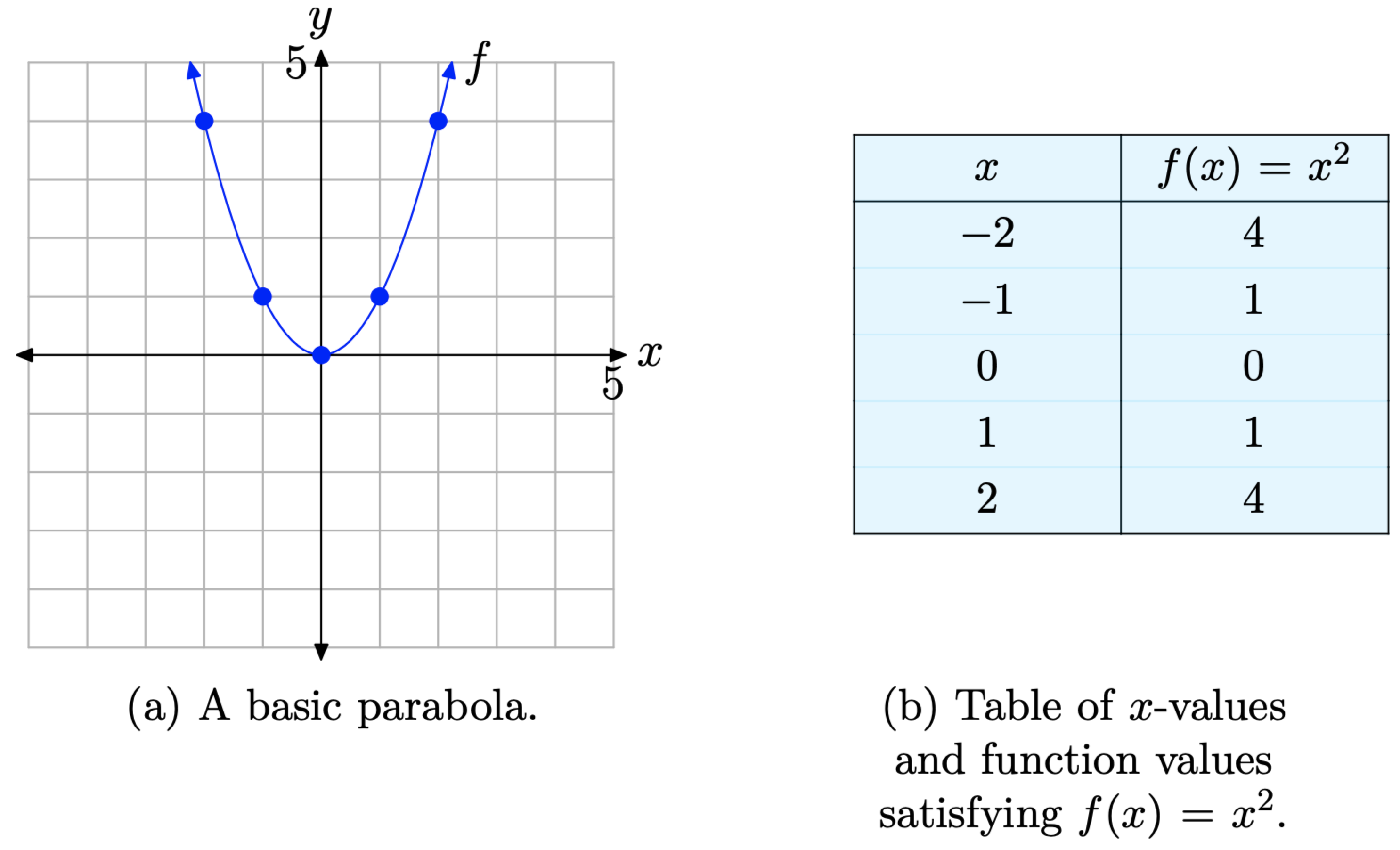
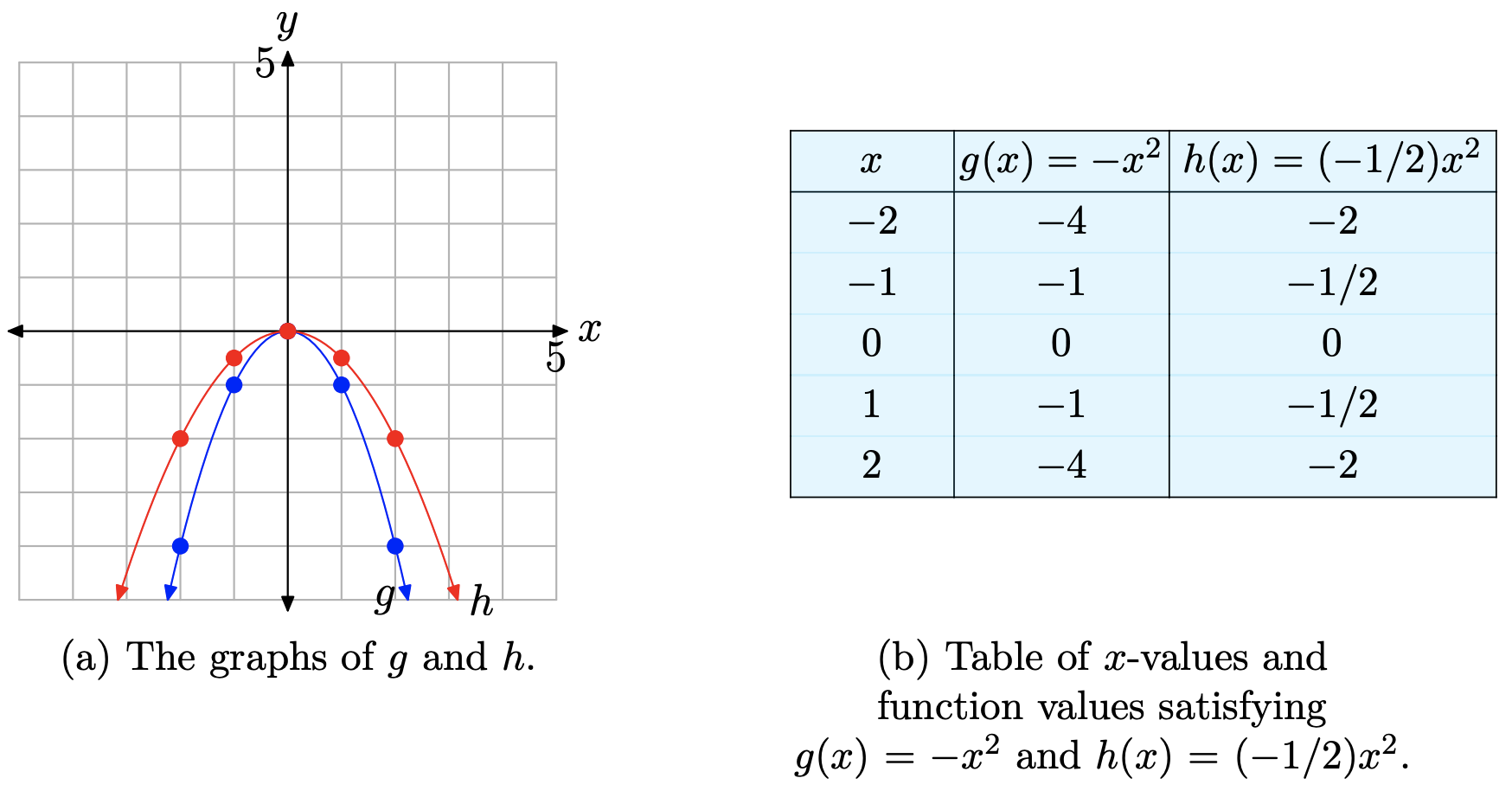
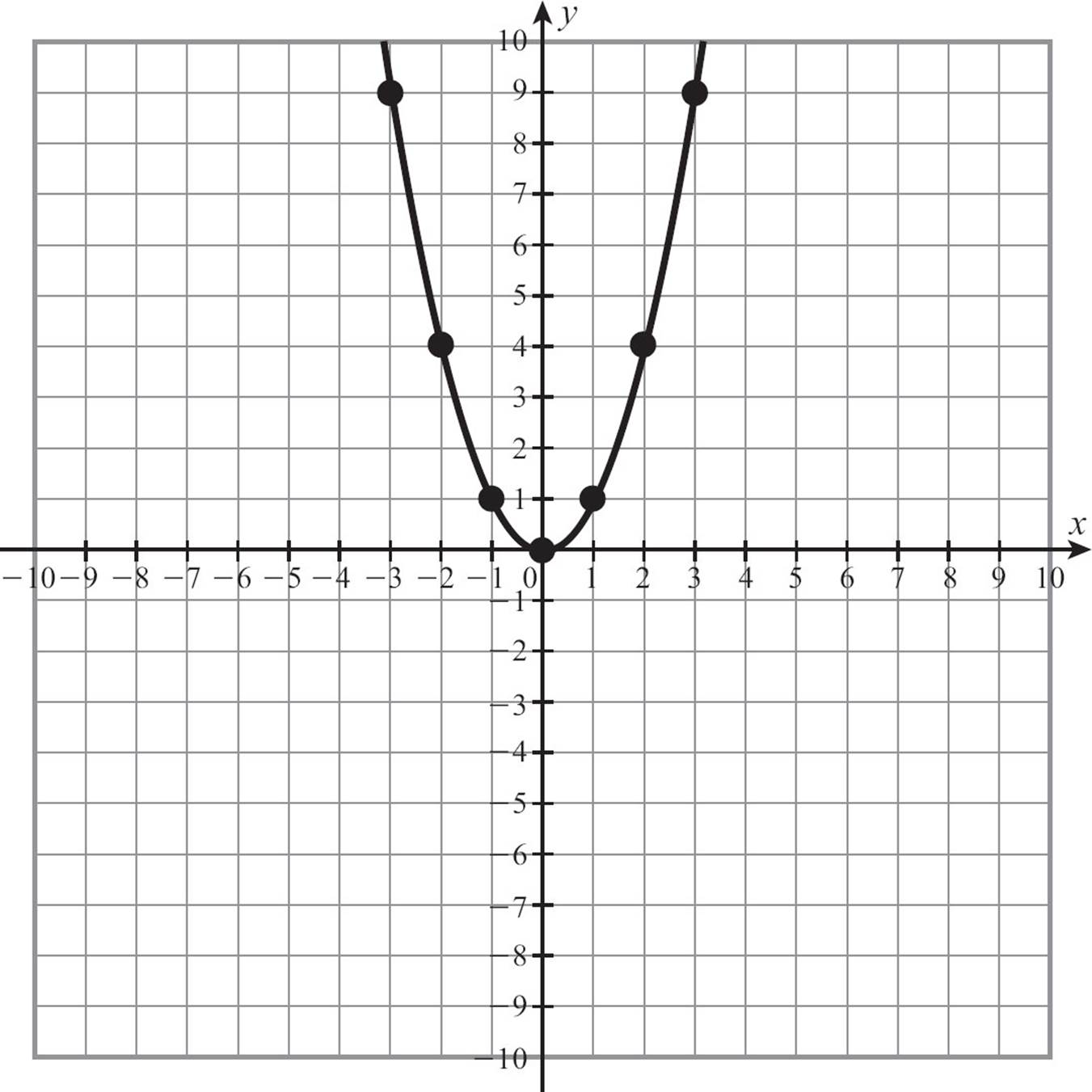
A ___ is the locus of points in a plane such that the difference of the distances to two fixed points called the foci is a constant hyperbola*** The ___ of a parabola is the point of a parabola lying halfway between the directrix and focus vertex The ___ of a parabola is the point, along with a line not containing the point, which isThe point at (0, 0), the "turning point" of the parabola, is called the vertex of the parabola We've tabulated a few points for reference in the table in Figure \(\PageIndex{1}\)(b) and then superimposed these points on the graph of \(f(x)=x^{2}\) in Figure \(\PageIndex{1}\)(a) Figure \(\PageIndex{1}\) The graph of the basic parabolaGraph the points and draw a smooth line through the points and extend it in both directions Notice that we have a minimum point which was indicated by a positive a value (a = 1) The vertex has the coordinates (1, 0) which is what you will get if you use the formula for the xcoordinate of the vertex



Ppt 4 3 Graphing Quadratic Equations And Its Transformations Powerpoint Presentation Id



Algebra 1 Section Ppt Download
A parabola which opens up has a lowest point and a parabola which opens down has a highest point The highest or lowest point on a parabola is called the vertex The parabola is symmetric about a vertical line through its vertex, called the axis of symmetrySurely you mean the point at which the parabola goes from increasing to decreasing, or reciprocally If y=ax^2bxc is a cartesian equation of a random parabola of the real plane, we know that in its turning point, the derivative is null An equatA turning point is a point where the graph of a function has the locally highest value (called a maximum turning point) or the locally lowest value (called a minimum turning point) A function does not have to have their highest and lowest values in turning points, though


Stationary Point Wikipedia



The Parabola Maths Grade 10 Rought Draft Openstax Cnx
Sideways Parabolas 1 Cool Math has free online cool math lessons, cool math games and fun math activities Really clear math lessons (prealgebra, algebra, precalculus), cool math games, online graphing calculators, geometry art, fractals, polyhedra, parents and teachers areas tooDefinition A parabola is a curve where any point is at an equal distance from a fixed point (the focus ), and a fixed straight line (the directrix ) Get a piece of paper, draw a straight line on it, then make a big dot for the focus (not on the line!)Rumble — There are 3 commonly used forms of writing a parabola This video deals with the 'Turning Point Form' Not a lengthy explanation nor lots of reasoning, just the basics This is good for the Australian Year 10A course and year 11 Methods or NSW Advanced Courses


Parabola Equations And Graphs Directrix And Focus And How To Find Roots Of Quadratic Equations Owlcation Education


Rate Of Increase Of A Quadratic Function Expii
Focus of a Parabola A parabola is set of all points in a plane which are an equal distance away from a given point and given line The point is called the focus of the parabola and the line is called the directrix The focus lies on the axis of symmetry of the parabola Finding the focus of a parabola given its equation If you have the equation of a parabola in vertex form y = a (x − hRumble — There are 3 commonly used forms of writing a parabola This video deals with the 'Turning Point Form' Not a lengthy explanation nor lots of reasoning, just the basics This is good for the Australian Year 10A course and year 11 Methods or NSW Advanced CoursesA parabola is a locus of points equidistant from both 1) a single point, called the focus of the parabola, and 2) a line, called the directrix of the parabola What is the Focus and Directrix?



Quadratic Function Wikipedia


Showme Parts Of A Parabola
A turning point may be either a local maximum or a minimum point If the function is smooth, then the turning point must be a stationary point, however not all stationary points are turning points, for example has a stationary point at x=0, but the derivative doesn't change sign as there is a point of inflexion at x=0 Curve sketchingWhat is the answer????What is the answer????



This Professor S Amazing Trick Makes Quadratic Equations Easier The New York Times



Parabola Equations And Graphs Directrix And Focus And How To Find Roots Of Quadratic Equations Owlcation Education
Equation of parabola is x^22xyy^22x10y5=0 Parabola is the locus of a point which moves so that its distance from a given point called focus and its distance from a given line called directrix is always equal Let the point be (x,y)During Polygraph Parabolas, Edwin asked this question "Is your parabola's turning point below the $$ xaxis?" (1) Use the sketch tool to indicate what Edwin is describing as the parabola's "turning point" (2) What other word or phrase could we use for "turning point"?The point half inbetween the directrix and focus is known as the vertex of the parabola Below is the figure of the parabola which is shown opening up and down It also appears in the right and left the plane The parabola is written in two forms standard form and vertex form y = ax^2 bx c (standard form) a, b, and c are coefficients
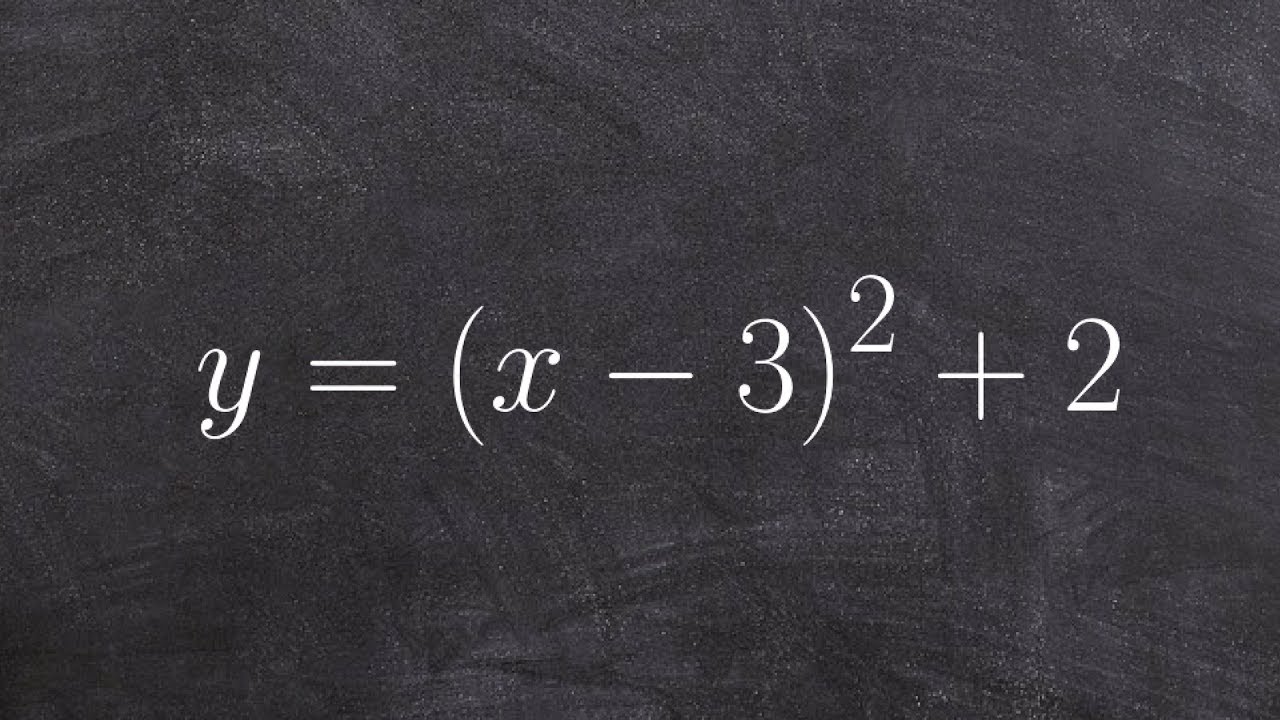


How To Graph A Parabola 13 Steps With Pictures Wikihow


5 1 The Parabola Mathematics Libretexts
The vertex of a parabola is the highest or lowest point, also known as the maximum or minimum of a parabola Properties of the Vertex of a Parabola is the maximum or minimum value of the parabola (see picture below) is the turning point of the parabolaDuring Polygraph Parabolas, Edwin asked this question "Is your parabola's turning point below the $$ xaxis?" (1) Use the sketch tool to indicate what Edwin is describing as the parabola's "turning point" (2) What other word or phrase could we use for "turning point"?Every parabola has an axis of symmetry and, as the graph shows, the graph to either side of the axis of symmetry is a mirror image of the other side This means that if we know a point on one side of the parabola we will also know a point on the other side based on the axis of symmetry


Parabola Equations And Graphs Directrix And Focus And How To Find Roots Of Quadratic Equations Owlcation Education



Parabola Equations And Graphs Directrix And Focus And How To Find Roots Of Quadratic Equations Owlcation Education
The graph below has a turning point (3, 2) Write down the nature of the turning point and the equation of the axis of symmetry The parabola shown has a minimum turning point at (3, 2) TheThe turning point of a parabola is called its?????Equation of the Axis of Symmetry of a Parabola The equation for the axis of symmetry of a parabola can be expressed as Remember that every quadratic function can be written in the standard form The graph of a quadratic function is called a parabola, where every point on that parabola represents an x and a y that solves the quadratic function
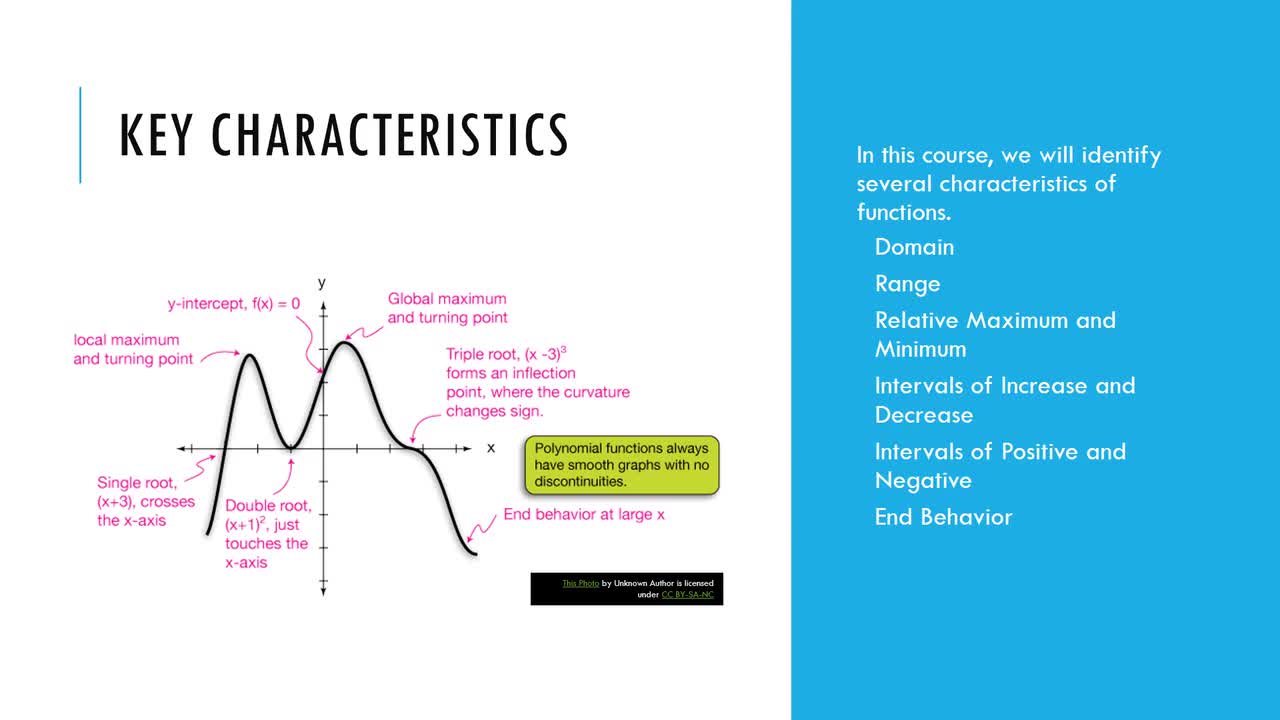


Domain And Range Ppt Video Riverdale High School



Thinking About U Theorizing And Testing U And Inverted U Shaped Relationships In Strategy Research Haans 16 Strategic Management Journal Wiley Online Library
The lowest point of a parabola The yvalue of the vertex when the parabola opens up xintercept The point(s) where a curve crosses the xaxis, also called a solution, root or zero of the function yintercept Where a curve crosses the yaxis Vertex The turning point of a quadratic function's graph Quadratic Formula A method used toThe result of the fraction is the xvalue of the ordered pair of the turning point of the parabola 4) Plug the xvalue into the original equation Your xvalue is 0 So, your new equation is y = 0^2 12 Now use algebra y = 0^2 12 y = 0 12 y = 12 5) Combine the x and y values to find the turning point of the parabola as an ordered pairA parabola is a locus of points equidistant from both 1) a single point, called the focus of the parabola, and 2) a line, called the directrix of the parabola What is the Focus and Directrix?



Graphing Quadratic Functions Day 2



The Parabola Algebra And Trigonometry
The most general form of a quadratic function is, f (x) = ax2 bx c f ( x) = a x 2 b x c The graphs of quadratic functions are called parabolas Here are some examples of parabolas All parabolas are vaguely "U" shaped and they will have a highest or lowest point that is called the vertexThe vertex is the turning point of the graph We can see that the vertex is at ( 3, 1) ( 3, 1) The axis of symmetry is the vertical line that intersects the parabola at the vertex So the axis of symmetry is latex x =3 /latex This parabola does not cross the x x axis, so it has no zerosThe distance of a point on the parabola from the focus is called the focal distance of the point (b) Focal chord A chord of the parabola, which passes through the focus is called a focal chord (c) Double ordinate A chord of the parabola perpendicular to the axis of the symmetry is called double ordinate (d) Latus rectum


Polynomial Types Of Polynomials Graphs Of Polynomials
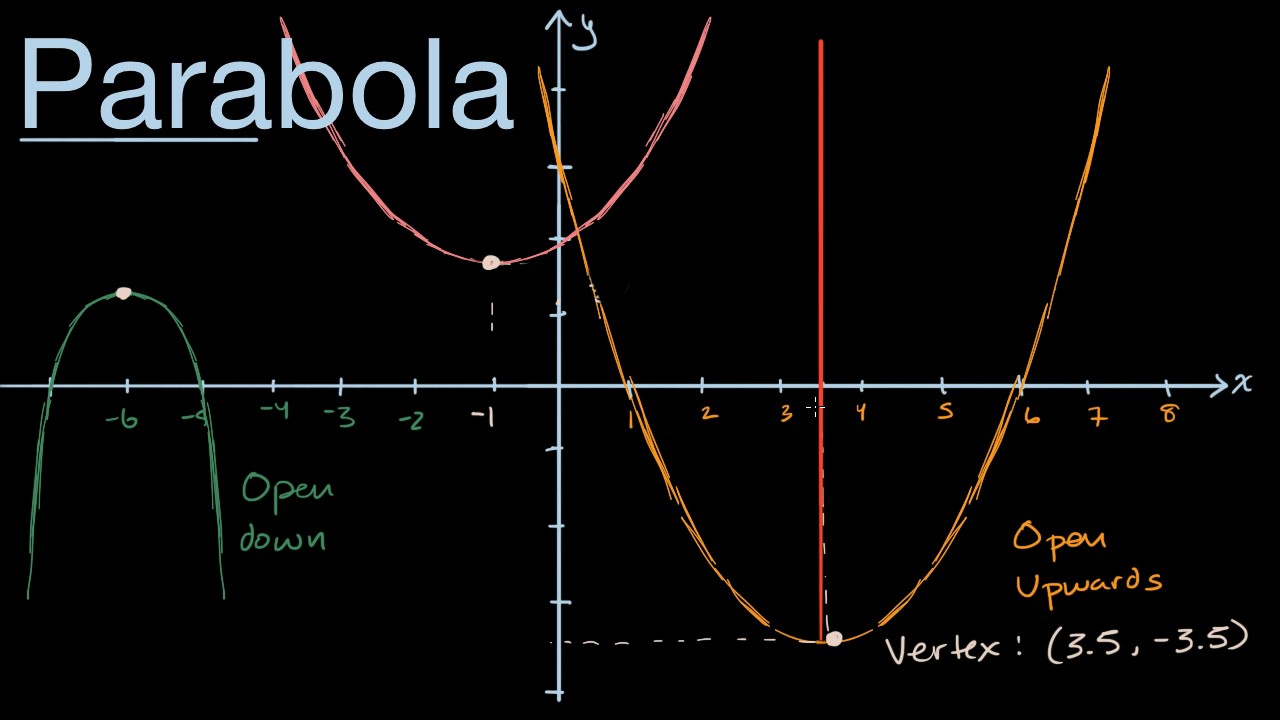


Parabolas Intro Video Intro To Parabolas Khan Academy
Turning Point 10 (b) y = —3x2 10 10 10 Turning Point Although the standard form of a parabola has advantages for certain applications, it is not helpful locating the most important point on the parabola, the turning point In this lesson, we will learn about a form of a parabola where the turning point is fairly obvoius QoockqcÞKQVertex of a parabola Quadratic functions are represented graphically by Ushaped curves called parabolas All parabolas are symmetric The axis of symmetry passes through the parabola at the vertexDuring Polygraph Parabolas, Edwin asked this question "Is your parabola's turning point below the $$ xaxis?" (1) Use the sketch tool to indicate what Edwin is describing as the parabola's "turning point" (2) What other word or phrase could we use for "turning point"?



This Professor S Amazing Trick Makes Quadratic Equations Easier The New York Times
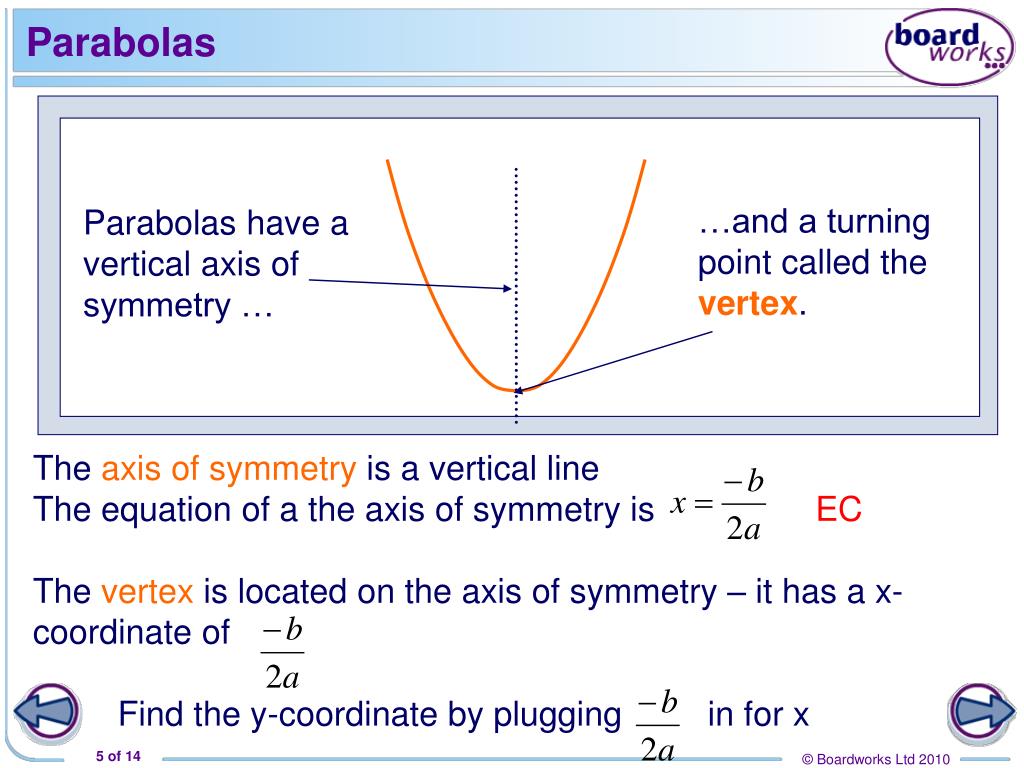


Ppt Graphs Parabolas By Calculating Strategic Points Powerpoint Presentation Id
The red point in the pictures below is the focus of the parabola and the red line is the directrix As you can see from the diagrams, when the focus isThe parabola opens upwards The minimum value of y is zero and it occurs when x = 0 The point (0, 0) is called the turning point or vertex of the parabola In general In the example above, a = 1 Example 2 Solution When we plot these points and join them with a smooth curve, we obtain the graph shown aboveThe vertical line that divides the parabola into two equal parts Vertex The turning point of a parabola Maximum A vertex that is the highest point Minimum A vertex that is the lowest point Solutions The point(s) at which the parabola intersect the xaxis x=b/2a The formula for the axis of symmetry
/GettyImages-547014049-57e296d85f9b5865161dff57.jpg)


What Are The Zeros Of A Quadratic Function
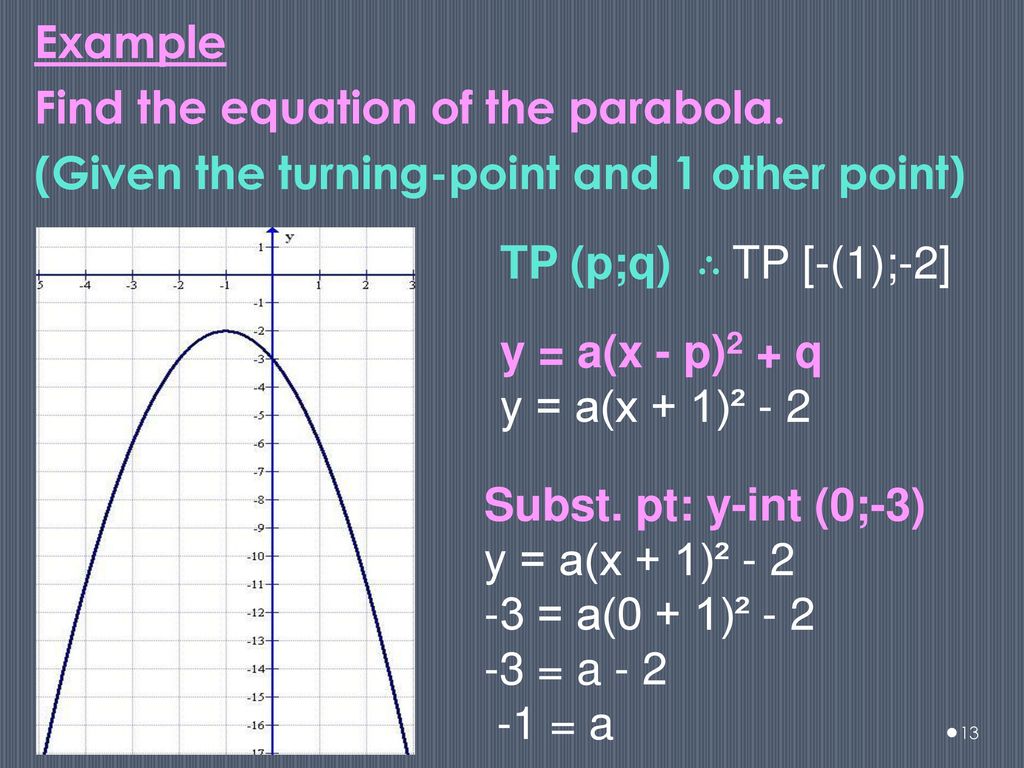


5 Functions Straight Lines Parabolas Hyperbolas Exponential Graphs Ppt Download
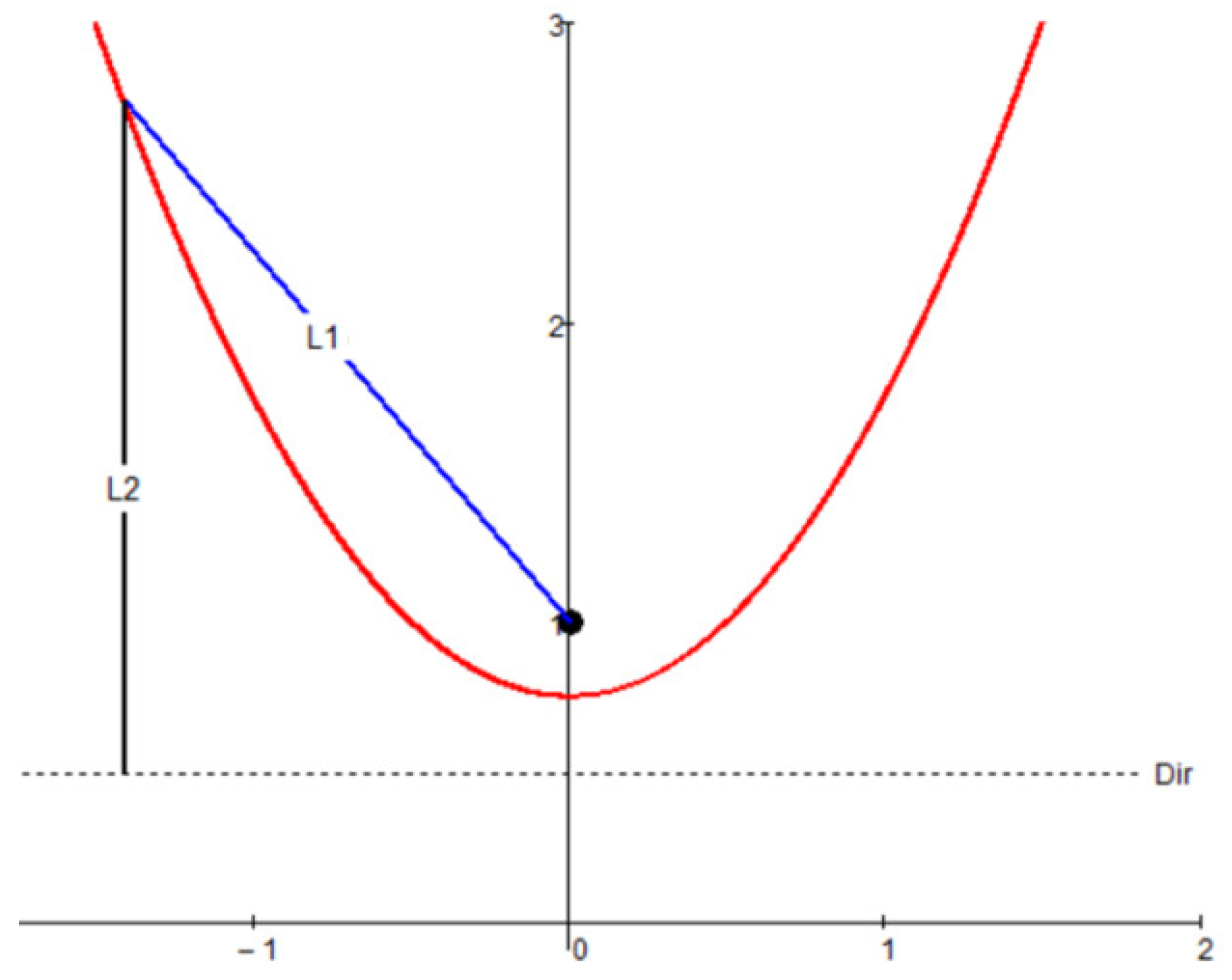
One way to do this is by using a parabolic reflector A parabola, shown in Figure 1, below, is a special mathematical shape — a curve consisting of the points that are equidistant from both a given fixed point called the focal point or ( focus) and a given fixed line (called the directrix ) Figure 1Answer Save 4 Answers Relevance roynburton Lv 5 1 decade ago Favorite Answer Vertex 1 0 Kathleen K Lv 7 1 decade ago Vertex 0 0 a_ebnlhaitham Lv 6 1 decade ago Head 0 0 enn Lv 6 1 decade ago What is an Apex, Alex Trebek 0 0 Still have questionsThe turning point of a parabola is called its?????



3 1 Quadratic Functions A Quadratic Function Is A


Quadratic Functions Radical Quadratic And Rational Functions Idiot S Guides Algebra I
A parabola has a directrix and a focus, a turning point, 0 1 or 2 roots and so on This extreme point on the parabola is called the vertex In math a parabola is a Ushaped curve with aThe red point in the pictures below is the focus of the parabola and the red line is the directrix As you can see from the diagrams, when the focus isAnswer Save 4 Answers Relevance roynburton Lv 5 1 decade ago Favorite Answer Vertex 1 0 Kathleen K Lv 7 1 decade ago Vertex 0 0 a_ebnlhaitham Lv 6 1 decade ago Head 0 0 enn Lv 6 1 decade ago What is an Apex, Alex Trebek 0 0 Still have questions
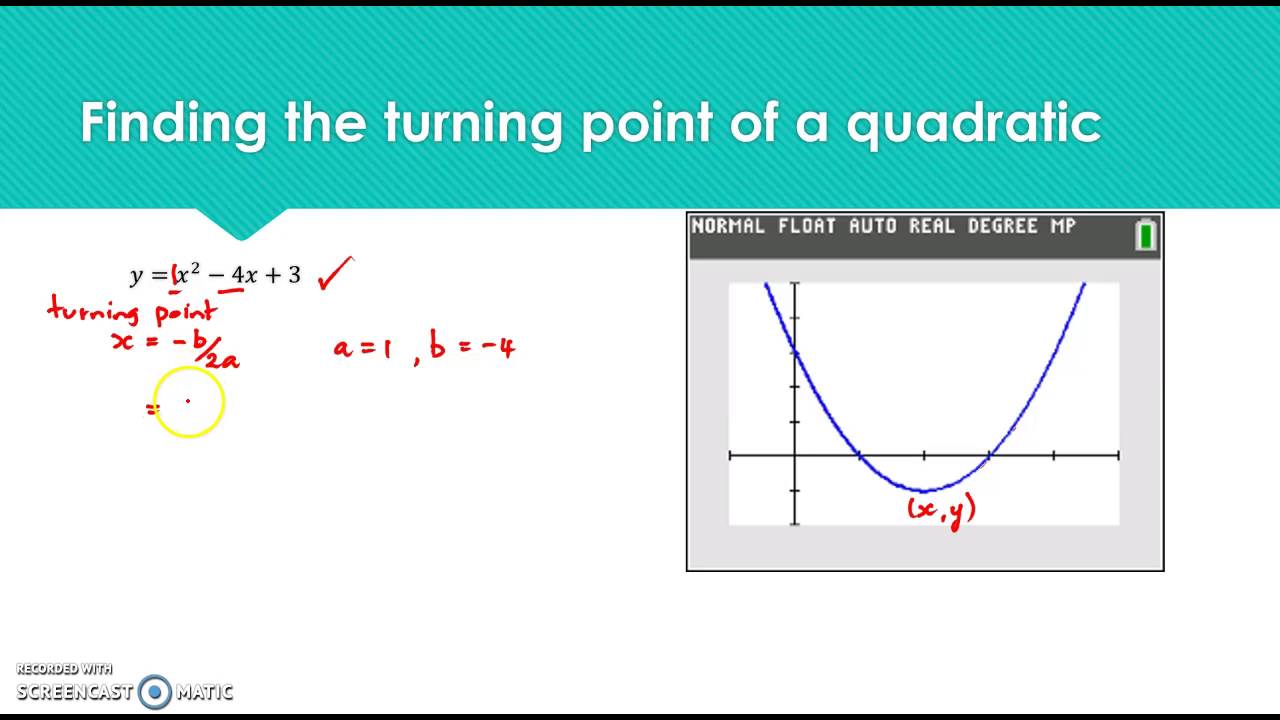


Finding The Turning Point Of A Quadratic Graph Youtube



Vertex Axis Of Symmetry Of A Parabola Video Khan Academy
At its basic, it is a set of all points that is equidistant to (1) a fixed point F called the focus, and (2) a fixed line called the directrix To expand, let's consider a point (x, y) as shown in the figure The distance between this point and F (d 1) should be equal to its perpendicular distance to the directrix (d 2)The following video shows one method of graphing parabolas Note that in this video the term vertex is used in place of turning point The vertex and the turning point are the same thing\n\n Khan academy video on graphing parabolas 1 \n\t \n\t \n\t \n\t Parabolas \n \n12 months ago The usual term for the "turning point" of a parabola is the VERTEX Differentiating y' = 2x 2 is the slope of the parabola at any point, depending on x The vertex is the only point at which the slope is zero, so we can solve 2x 2 = 0 2x = 2 adding 2 to each side x = 1 dividing each side by 2


How To Find The Equation Of A Parabola Given The Turning Point


Symmetry Free Full Text A New Ellipse Or Math Porcelain Service Html
Find the parabola's Vertex, or "turning point", which is found by using the value obtained finding the axis of symmetry and plugging it into the equation to determine what y equals Find the Roots, or XIntercepts, by solving the equation and determining the values for x when f(x) = f(0) = y = 0



Quadratic Functions In Chapter 3 We Will Discuss Polynomial Functions Ppt Download


5 1 The Parabola Mathematics Libretexts



How To Draw A Parabola Ppt Download



Parabola As A Locus Youtube



Higher Polynomials And Quadratics 64 Pdf Free Download
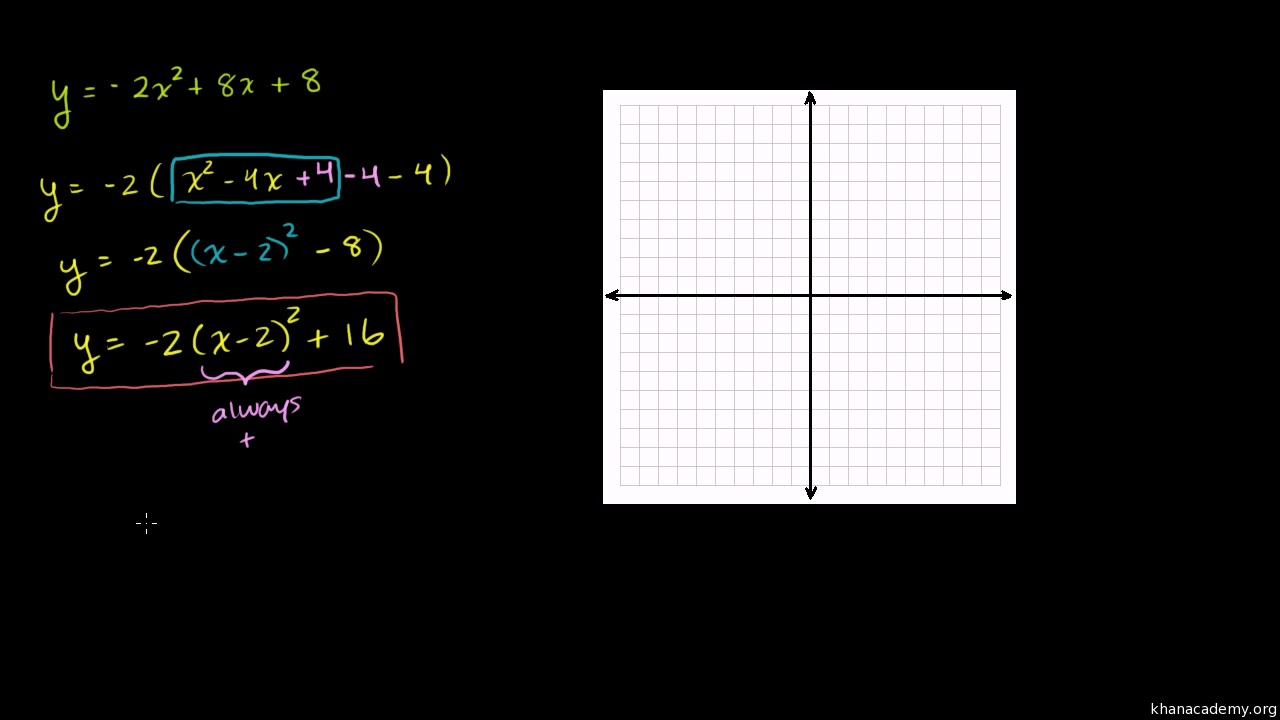


Vertex Axis Of Symmetry Of A Parabola Video Khan Academy
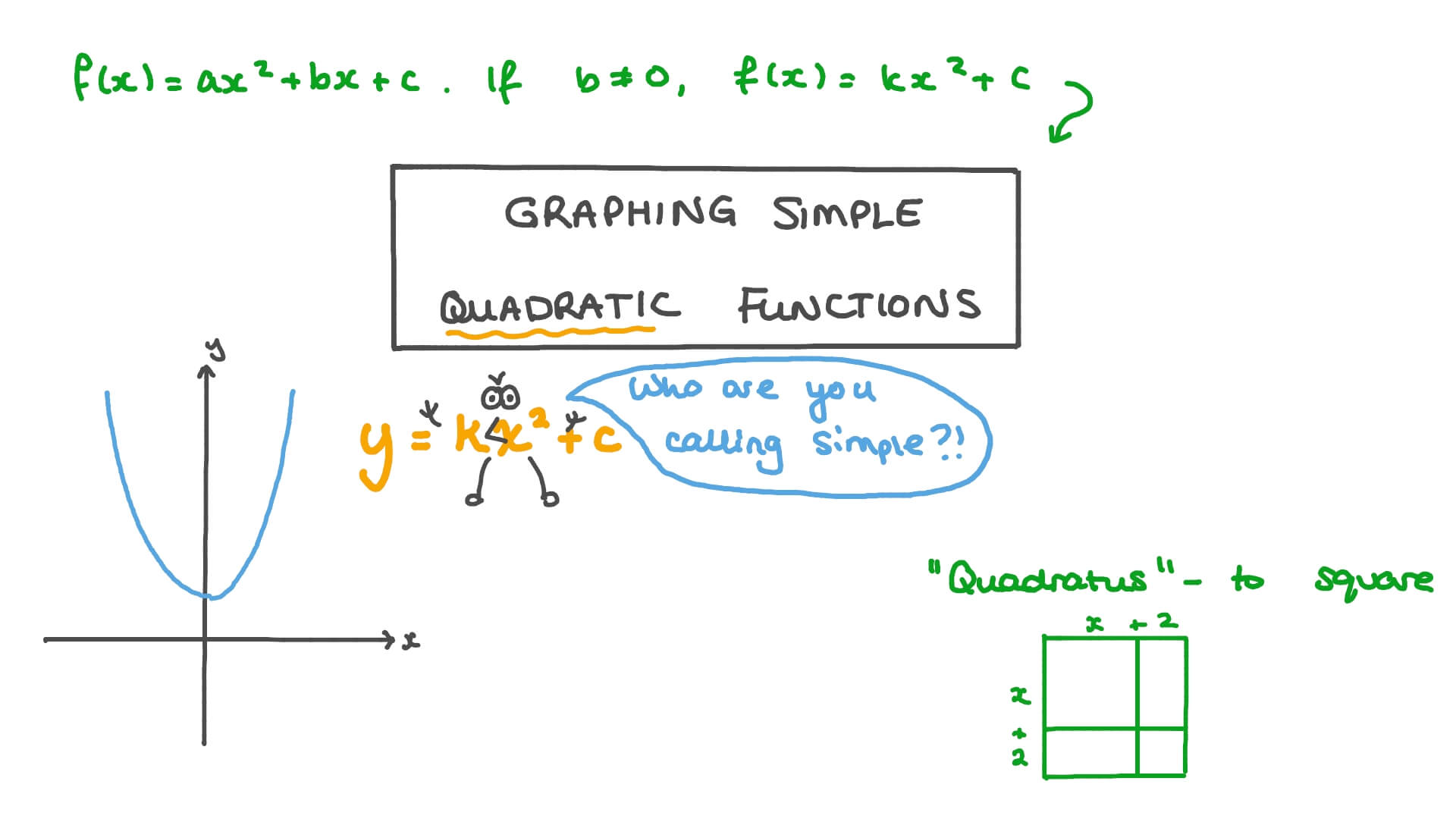


Lesson Video Graphing Simple Quadratic Functions Nagwa



Parabolas And The Distance Formula Read Calculus Ck 12 Foundation



How To Graph A Parabola 13 Steps With Pictures Wikihow



Mac 1105 3 1 Graphing Quadratic Functions Studocu
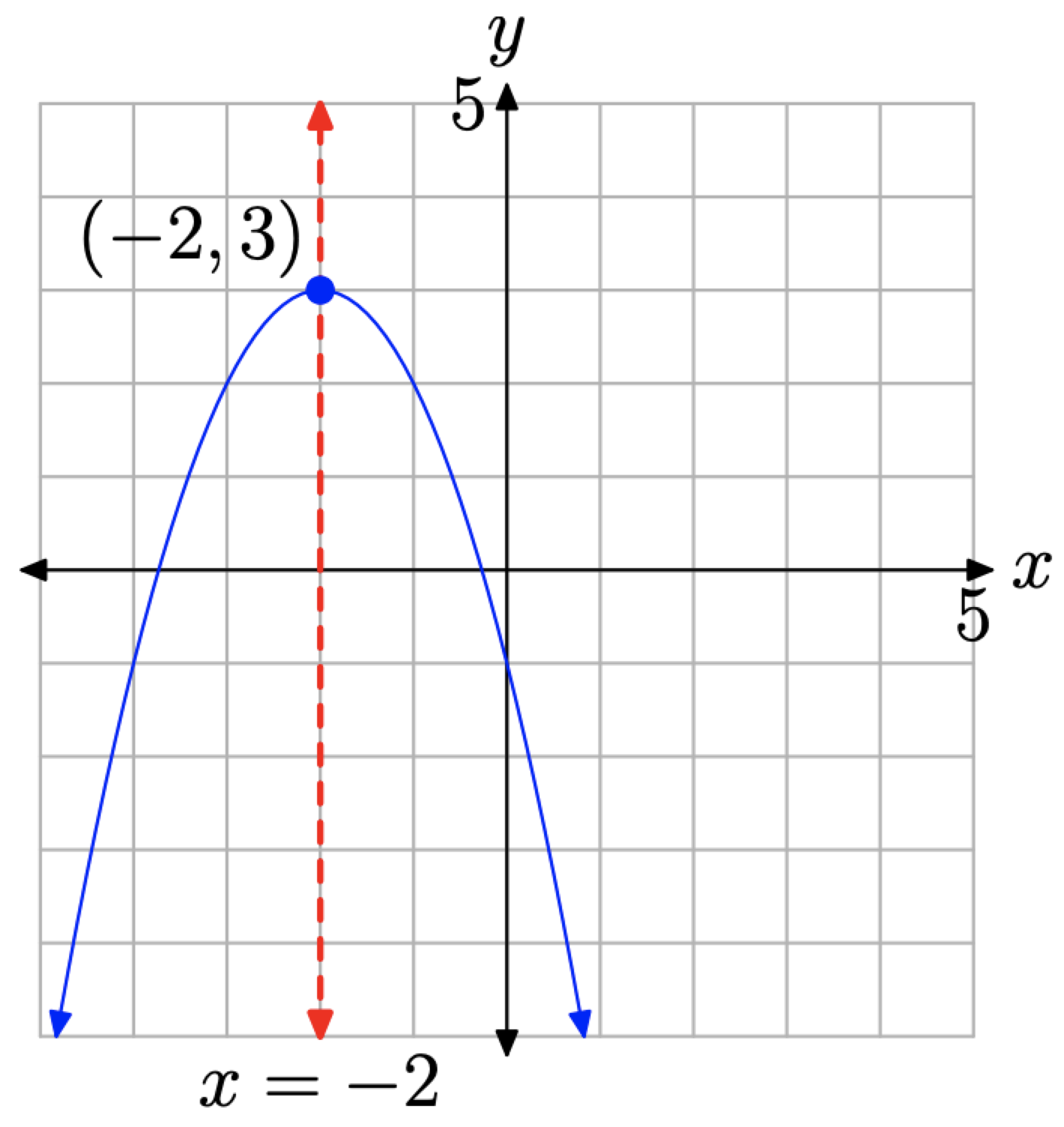


5 1 The Parabola Mathematics Libretexts
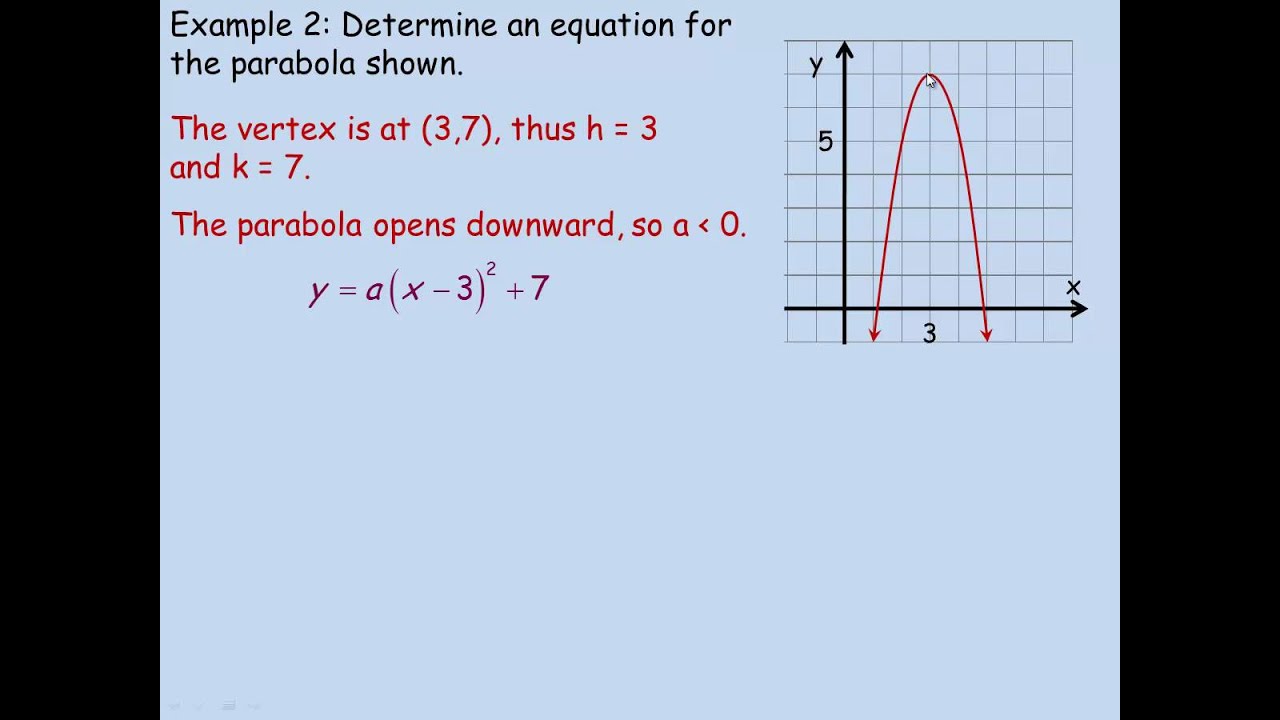


Graphing Y A X H K Youtube



Vertex Form For Parabolas
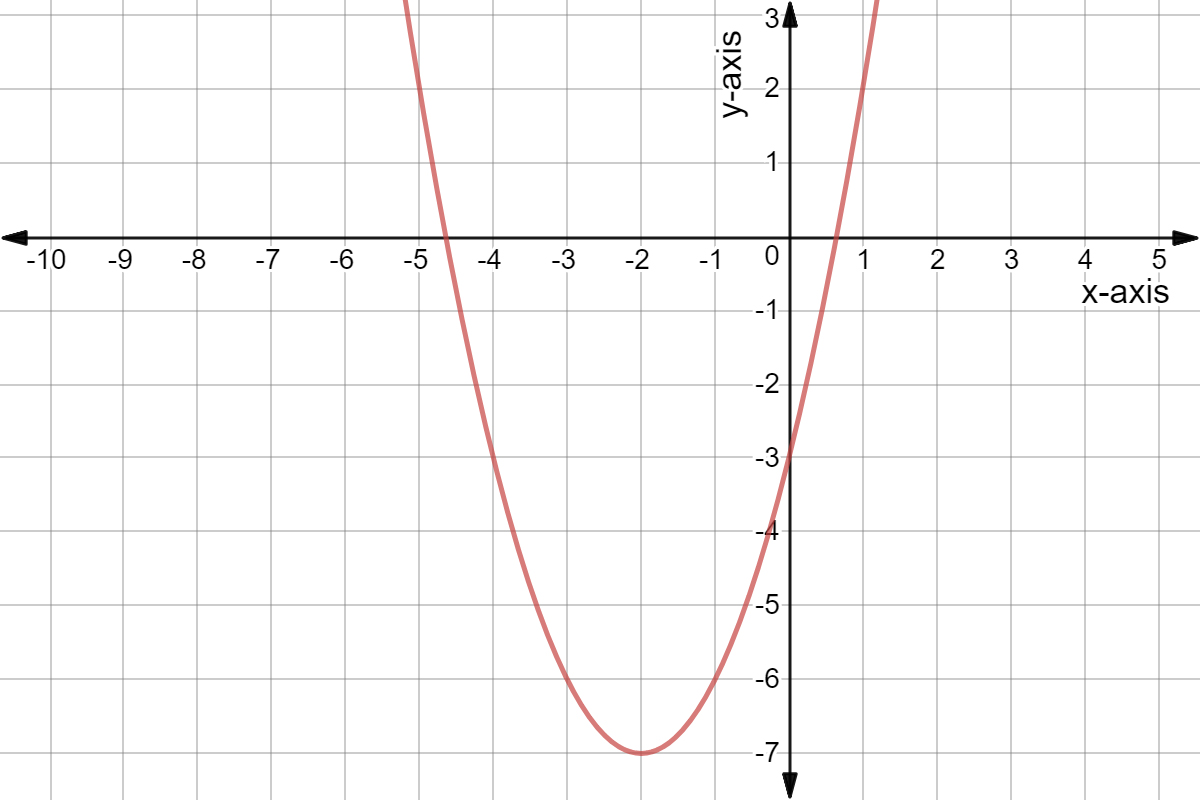


Completing The Square Vertex Form Of A Quadratic Expii
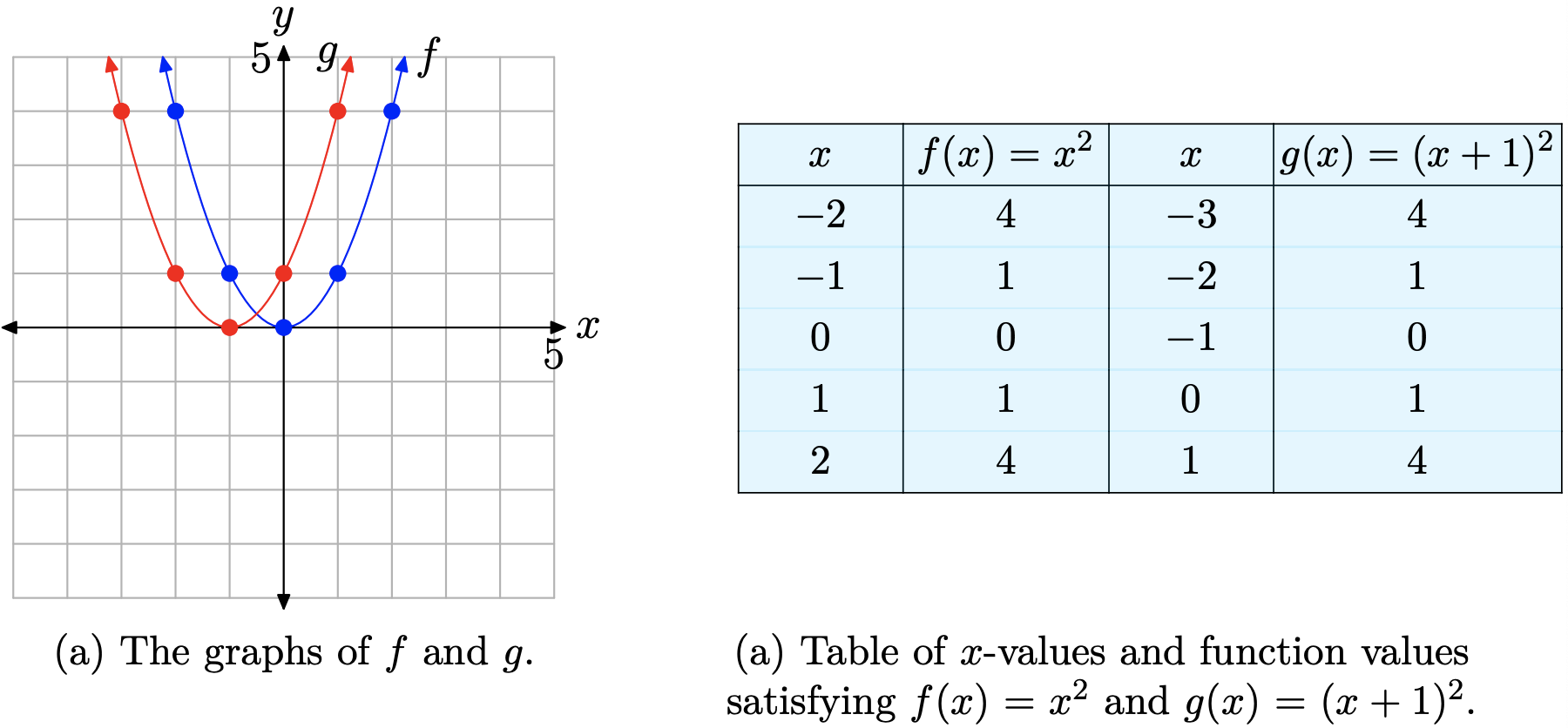


5 1 The Parabola Mathematics Libretexts
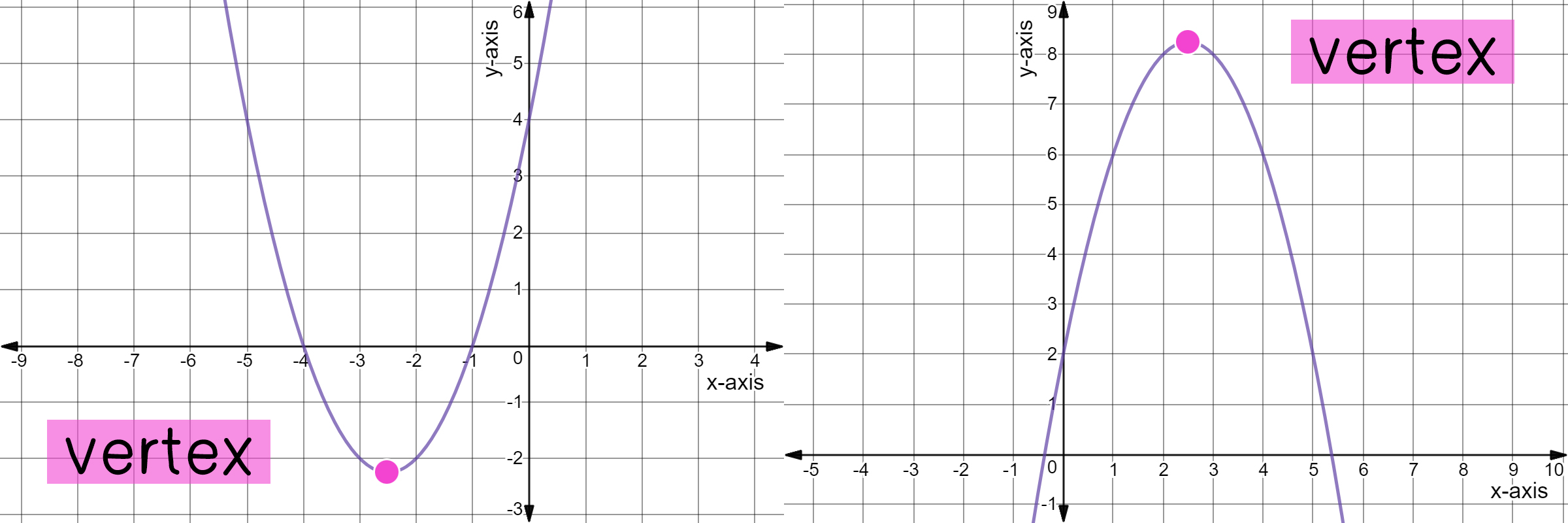


Completing The Square Vertex Form Of A Quadratic Expii



Parabolas And The Distance Formula Read Calculus Ck 12 Foundation



Pdf A Note On The Turning Point For The Quadratic Trend
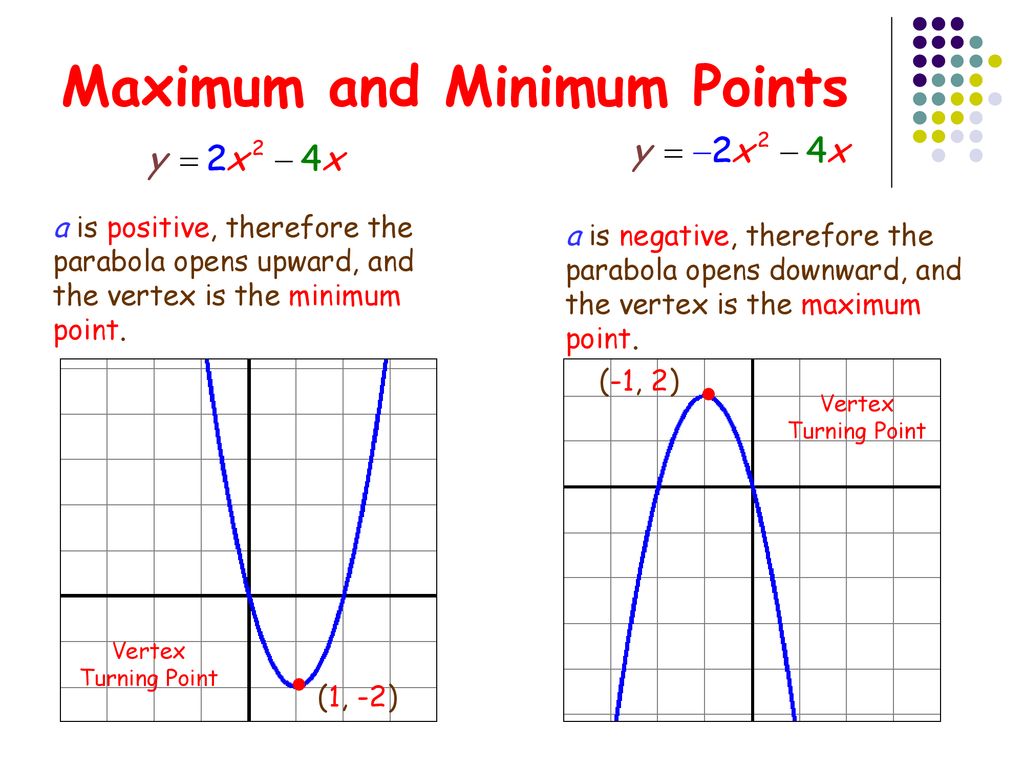


Exploring Quadratic Functions Ppt Download



5 1 The Parabola Mathematics Libretexts



Higher Polynomials And Quadratics 64 Pdf Free Download



Parabolas And The Distance Formula Read Calculus Ck 12 Foundation



How To Find The Equation Of A Parabola Given The Turning Point



1 What Is The Opening Of The Parabola 2 What Are The Coordinates Of The Turning Point Of The Brainly Ph



Lesson 23 Quadratic Functions Studocu


Relations And Functions Media4math



0 件のコメント:
コメントを投稿